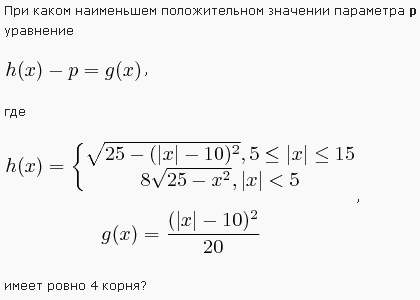
Беглый осмотр невооруженным глазом приводит нас к неутешительной мысли о необходимости решения как минимум двух уравнений 4-й степени. Они, конечно, как-то решаются, но все это долго, скучно и занудно.
А теперь посмотрим за задачу воруженным глазом и обнаружим, что график функции h(x) (дальше будем звать его Х) представляет собой две полуокружности радиусом 5 и центрами в точках (-10,0) и (10,0), и полуэллипс с горизонтальной полуосью 5, вертикальной полуосью 40 и центром в точке (0,0).
В свою очередь, график функции g(x) (дальше будем звать его Ж) — это часть параболы, задаваемой выражением 0.05(x–10)2, расположенная в правой полуплоскости, зеркально отраженная на левую полуплоскость.
Изменение же параметра p в нашем исходном уравнении можно графически изобразить как простое смещение Х относительно Ж вдоль вертикальной оси. Гораздо понятнее все это становится при взгляде на следующий рисунок:
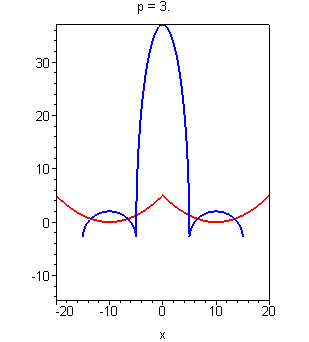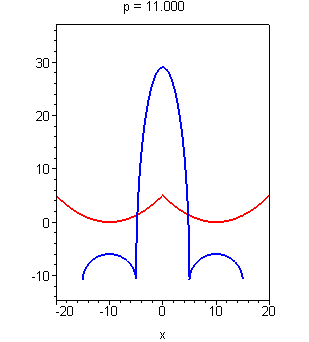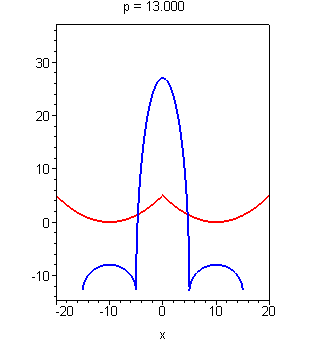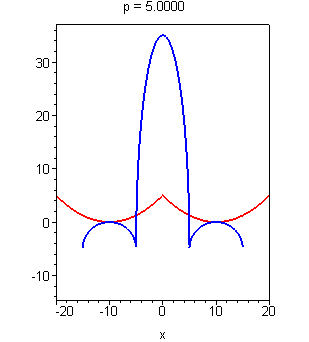
Ответ очевиден — p = 5. Это не единственный случай, когда уравнение имеет ровно 4 корня, но нам, как мы помним, нужно наименьшее положительное значение. Аккуратное математическое обоснование этого ответа не займет особого труда и я не вижу смысла здесь его приводить.
